莫比乌斯反演

orz hhw posted @ 2015年6月11日 17:30 in 算法学习 with tags 模板数论莫比乌斯反演算法学习 , 4642 阅读

基本内容：

线性求莫比乌斯函数模板：

#include<cstdio>
#define N 10000000
using namespace std;
int i,j,n,p,ans,R,cnt[N],prime[N],phi[N],u[N];
bool f[N];
int main(){
	scanf("%d",&n);scanf("%d",&R);//R为逆元模 
	u[1]=1;
	for(i=2;i<=n;i++){
        if(!f[i]){
            prime[++p]=i;//prime存素数 
            cnt[i]=1;//cnt为因数个数 
            phi[i]=i-1;//phi为欧拉函数 
            u[i]=-1;//u为莫比乌斯函数 
        }
        for(j=1;j<=p&&i*prime[j]<=n;j++){
            f[i*prime[j]]=1;
            cnt[i*prime[j]]=cnt[i]+1;
            if(i%prime[j]==0){
				phi[i*prime[j]]=phi[i]*prime[j];
				break;
	   		}
	    	phi[i*prime[j]]=phi[i]*(prime[j]-1);
	    	u[prime[j]*i]=-u[i];
        }
    }
}

BZOJ2301：莫比乌斯函数另一种形式+前缀和

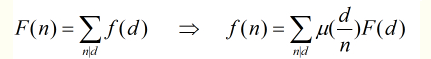
i-(n/(n/i))可以取出和n/i商相同的值快速更新答案

#include<cstdio>
#include<iostream>
#define N 111111
using namespace std;
long long i,j,T,a,b,c,d,k,last,p,u[N],sum[N],prime[N];
bool f[N];
long long calc(long long n,long long m){
	n/=k;m/=k;
	long long re=0;
	for(long long i=1;i<=min(n,m);i=last+1){
		last=min(n/(n/i),m/(m/i));
		re+=(n/i)*(m/i)*(sum[last]-sum[i-1]);
	}
	return re;
}
int main(){
	sum[1]=u[1]=1;
	for(i=2;i<N;i++){
		if(!f[i]){
			prime[++p]=i;
			u[i]=-1;
		}
		for(j=1;j<=p&&i*prime[j]<N;j++){
			f[i*prime[j]]=1;
			if(i%prime[j])u[prime[j]*i]-=u[i];
			else break;
		}
		sum[i]=sum[i-1]+u[i];
	}
	scanf("%lld",&T);
	while(T--){
		scanf("%lld%lld%lld%lld%lld",&a,&b,&c,&d,&k);
		printf("%lld\n",calc(b,d)+calc(a-1,c-1)-calc(a-1,d)-calc(b,c-1));
	}
}

#include<cstdio>
#include<algorithm>
#define N 50050
using namespace std;
int n,m,i,j,pos,ans,t,Q,x,y,z,p[N],sum[N],u[N];bool f[N];
int main(){
	for(n=50000,sum[1]=u[1]=1,i=2;i<=n;i++){
		if(!f[i])p[++t]=i,u[i]=-1;
		for(j=1;j<=t&&i*p[j]<=n;j++){
			f[i*p[j]]=1;
			if(i%p[j])u[i*p[j]]=-u[i];else break;
		}
		sum[i]=sum[i-1]+u[i];
	}
	for(scanf("%d",&Q);Q--;printf("%d\n",ans),ans=0){
		scanf("%d%d%d",&x,&y,&z);n=x/z;m=y/z;if(n>m)swap(n,m);
		for(i=1;i<=n;i=pos+1){
			pos=min(n/(n/i),m/(m/i));
			ans+=(sum[pos]-sum[i-1])*(n/i)*(m/i);
		}
	}
}

BZOJ2820 枚举每个质数，那么答案和上题一样求，可是这样会T

使pd=T，那么ans=Σ(n/T)(m/T)Σu(T/p)(p|T)，这样预处理使得时间复杂度变为O(n+qn^0.5)

#include<bits/stdc++.h>
#define N 10001000
using namespace std;
int i,j,t,T,n,m,la,p[N],sum[N],u[N];long long ans;bool f[N];
int main(){
	for(u[1]=1,i=2;i<N;i++){
		if(!f[i])p[++t]=i,u[i]=-1;
		for(j=1;j<=t&&i*p[j]<N;j++){
			f[i*p[j]]=1;
			if(i%p[j]==0)break;
			u[i*p[j]]=-u[i];
		}
	}
	for(j=1;j<=t;j++)for(i=p[j];i<N;i+=p[j])sum[i]+=u[i/p[j]];
	for(i=1;i<N;i++)sum[i]+=sum[i-1];
	for(scanf("%d",&T);T--;printf("%lld\n",ans),ans=0)
		for(scanf("%d%d",&n,&m),i=1;i<=min(n,m);i=la+1)
			ans+=(long long)(n/i)*(m/i)*(sum[la=min(n/(n/i),m/(m/i))]-sum[i-1]);
}

BZOJ3529 用g(i)表示1≤x≤n，1≤y≤m，gcd(x,y)=i的个数，那么g(i)=Σu(d/i)*(n/d)*(m/d)

可得公式ans=ΣF(i)g(i)=(n/d)*(m/d)*ΣF(i)Σu(d/i)，现在只需要求出ΣF(i)Σu(d/i)的前缀和即可

如果F(i)没有限制，那么可以O(nlgn)前缀和预处理，O(n^0.5)处理每个询问

现在有限制，可与对F(i)和所有a排序，对于每个询问a只把F(i)≤a的加入树状数组中，这样维护前缀和，总时间复杂度O(nlg^2n+qn^0.5lgn)

#include<bits/stdc++.h>
#define N 100100
using namespace std;
int i,j,k,t,T,u[N],p[N],c[N],ans[N];bool f[N];
struct P{int x,y,z,id;}e[N],q[N];bool cmp(P a,P b){return a.z<b.z;}
void add(int x,int z){for(;x<N;x+=x&-x)c[x]+=z;}
int qu(int x){int sum=0;for(;x;x-=x&-x)sum+=c[x];return sum;}
int get(int n,int m){
	int i,la,sum=0;
	for(i=1;i<=min(n,m);i=la+1)sum+=(n/i)*(m/i)*(qu(la=min(n/(n/i),m/(m/i)))-qu(i-1));
	return sum&2147483647;
}
int main(){
	for(u[1]=1,i=2;i<N;i++){
		if(!f[i])p[++t]=i,u[i]=-1;
		for(j=1;j<=t&&i*p[j]<N;j++){
			f[i*p[j]]=1;
			if(i%p[j]==0)break;
			u[i*p[j]]=-u[i];
		}
	}
	for(i=1;i<N;e[i].x=i++)for(j=i;j<N;j+=i)e[j].z+=i;
	for(sort(e+1,e+N,cmp),scanf("%d",&T),i=1;i<=T;q[i].id=i++)scanf("%d%d%d",&q[i].x,&q[i].y,&q[i].z);
	for(sort(q+1,q+T+1,cmp),i=j=1;i<=T;ans[q[i].id]=get(q[i].x,q[i].y),i++)
		for(;j<N&&e[j].z<=q[i].z;j++)for(k=e[j].x;k<N;k+=e[j].x)add(k,e[j].z*u[k/e[j].x]);
	for(i=1;i<=T;i++)printf("%d\n",ans[i]);
}

BZOJ2154 ans=(i=1~n,j=1~m)Σij/gcd(i,j)，令d=gcd(i,j),F(x,y)=(i=1~x,j=1^y,gcd(i,j)=1)Σij

那么可以得到ans=(d=1~min(n,m))Σd^2F(n/d,m/d)/d=ΣdF(n/d)(m/d)

然后对F(x,y)进行反演，F(x,y)=(d=1~min(x,y))Σu(d)Σi(d|i=1~x)Σj(d|j=1~y)=(d=1~min(x,y))Σu(d)d^2Σi(i=1~x/d)Σj(j=1~y/d)=(i=1~min(x,y))Σi^2u(i)(i=1~x,j=1^y)Σij

而很明显2u(i)(i=1~x,j=1^y)Σij=i*(i-1)/2*j*(j-1)/2

这样两个公式都可以n^0.5求出，总时间复杂度O(n)

#include<bits/stdc++.h>
#define N 10010000
#define M 20101009  
using namespace std;typedef long long LL;
int i,j,t,n,m,la,u[N],p[N];LL ans,sum[N];bool f[N];
LL O(LL x){return (x*(x+1)/2)%M;}
LL F(int x,int y){
	int i,la;LL re=0;
	for(i=1;i<=min(x,y);i=la+1)re=(re+O(x/i)*O(y/i)%M*(sum[la=min(x/(x/i),y/(y/i))]-sum[i-1]))%M;
	return re;
}
int main(){
	for(sum[1]=u[1]=1,i=2;i<N;i++){
		if(!f[i])p[++t]=i,u[i]=-1;
		for(j=1;j<=t&&i*p[j]<N;j++){
			f[i*p[j]]=1;if(i%p[j]==0)break;
			u[i*p[j]]=-u[i];
		}
		sum[i]=(sum[i-1]+(LL)i*i*u[i])%M;
	}
	for(scanf("%d%d",&n,&m),i=1;i<=min(n,m);i=la+1)ans=(ans+F(n/i,m/i)*(O(la=min(n/(n/i),m/(m/i)))-O(i-1)+M))%M;
	printf("%lld",ans);
}

BZOJ2693 上面一题的多组询问版，考虑继续简化公式

ans=(d=1~min(n,m))Σd(i=1~min(n,m)Σi^2u(i)sum(n/di,m/di),设D=di

则ans=(D=1~min(n,m))ΣF(n/D,m/D)(i|D)ΣDi·u(i)

那么只需要对ΣDi·u(i)求出前缀和，就可以在O(n^0.5)的时间内处理每个询问

而由于这是一个奇性函数，可以线性筛时处理出来

#include<bits/stdc++.h>
#define N 10010000
#define M 100000009
using namespace std;typedef long long LL;
int i,j,t,n,m,T,la,p[N];LL ans,sum[N],u[N];bool f[N];
LL O(LL x){return (x*(x+1)/2)%M;}
int main(){
	for(sum[1]=u[1]=1,i=2;i<N;i++){
		if(!f[i])p[++t]=i,u[i]=(i-(LL)i*i)%M;
		for(j=1;j<=t&&i*p[j]<N;j++){
			f[i*p[j]]=1;
			if(i%p[j]==0){
				u[i*p[j]]=p[j]*u[i]%M;
				break;
			}
			u[i*p[j]]=u[p[j]]*u[i]%M;
		}
		sum[i]=(sum[i-1]+u[i])%M;
	}
	for(scanf("%d",&T);T--;printf("%lld\n",(ans+M)%M),ans=0)
		for(scanf("%d%d",&n,&m),i=1;i<=min(n,m);i=la+1)
			ans=(ans+O(n/i)*O(m/i)%M*(sum[la=min(n/(n/i),m/(m/i))]-sum[i-1]))%M;
}

BZOJ3944 打BC的时候最后时候推出莫比乌斯发现n=1e9没法快速前缀和，记得看到过BZOJ上一道题可以O(n^2/3)求莫比乌斯前缀和，就向Claris问到题号抄程序贴上去A了。比赛完再把这题看了下，大概就是≤n^2/3的预处理，大于n^2/3的递归后MAP快速出解。

#include<bits/stdc++.h>
#define M 4000000
using namespace std;typedef long long LL;
int n,i,j,x,p,T,pr[M],u[M];bool f[M];LL phi[M];map<int,LL>mp,mo;
LL P(int n){
	if(n<M)return phi[n];if(mp.count(n))return mp[n];
	LL x=1ll*n*(n+1)/2;
	for(int i=2,la;i<=n;i=la+1)la=n/(n/i),x-=P(n/i)*(la-i+1);
	return mp[n]=x;
}
LL U(int n){
	if(n<M)return u[n];
	if(mo.count(n))return mo[n];
	LL x=1,i=2,la;
	for(i=2,la;i<=n;i=la+1)la=n/(n/i),x-=U(n/i)*(la-i+1);
	return mo[n]=x;
}
int main(){
	for(phi[1]=u[1]=1,i=2;i<M;i++){
		if(!f[i])pr[++p]=i,phi[i]=i-1,u[i]=-1;
    	for(j=1;j<=p&&i*pr[j]<M;j++){
       		f[i*pr[j]]=1;
        	if(i%pr[j]==0){
        		u[pr[j]*i]=0;
        		phi[i*pr[j]]=phi[i]*pr[j];
        		break;
        	}
        	phi[i*pr[j]]=phi[i]*(pr[j]-1);
        	u[pr[j]*i]=-u[i];
    	}
	}
	for(i=2;i<M;i++)u[i]+=u[i-1],phi[i]+=phi[i-1];
	for(scanf("%lld",&T);T--;printf("%lld %lld\n",P(x),U(x)))scanf("%d",&x);
}

BZOJ4407 ans=Σ(i<=n)Σ(j<=m)gcd(i,j)^k=Σd^kΣ(i<=n/d)Σ(j<=m/d)gcd(i,j)=1

=Σd^kΣu(w)*(n/wd)*(m/wd)=Σ(n/D)(m/D)Σ(d|D)d^k*(u(D/d))

由于快速幂Log消不掉，就暴力求吧。。

#include<bits/stdc++.h>
#define M 1000000007
#define N 5000001
using namespace std;typedef long long LL;bool f[N];int T,n,m,k,i,j,t,u[N],p[N];LL ans,v,F[N],h[N];
LL pow(LL a,LL b,LL p){for(v=1;b;a=a*a%p,b>>=1)if(b&1)v=v*a%p;return v;}
int main(){
	for(scanf("%d%d",&T,&k),i=2;i<N;i++){
		h[i]=pow(i,k,M);if(!f[i])p[++t]=i,F[i]=h[i]-1;
		for(j=1;j<=t&&i*p[j]<N;j++){
			f[i*p[j]]=1;
			if(i%p[j])F[i*p[j]]=(F[i]*(h[p[j]]-1))%M;else{F[i*p[j]]=F[i]*h[p[j]]%M;break;}
		}
	}
	for(F[1]=1,i=2;i<N;i++)F[i]=(F[i]+F[i-1])%M;
	for(;T--;printf("%lld\n",ans))for(scanf("%d%d",&n,&m),ans=0,i=1;i<=min(n,m);i=j+1)j=min(n/(n/i),m/(m/i)),ans=(ans+(F[j]-F[i-1]+M)*(n/i)%M*(m/i))%M;
}

BZOJ3309 枚举d=gcd(i,j)，得到

。

如果求出的前缀和就可以O()得到每组答案。

令T=p1^a¹*p2^a²*…*pk^ak，d=p1^b1*p2^b2*…*pk^bk，0<=ai-bi<=1。

发现如果存在ai!=aj，那么g(T)=0。否则g(T)=(-1)^k+1。

BZOJ3512 设。那么在时，有。

两边求和得

对于的情况，找到最大的k|n使得，。

特殊地，。对较小的进行预处理，然后记忆化搜索得到答案。

#include<bits/stdc++.h>
#define N 4500000
#define M 1000000007
#define pm make_pair
using namespace std;typedef long long LL;LL w,ans;map<pair<LL,LL>, LL>mp;
bool f[N];int i,j,t,n,m,u[N],phi[N],p[N],to[N],sm[N];
LL P(LL n,LL m){
	if(!m)return 0;if(n==1&&m<N)return sm[m];
	if(mp.count(pm(n,m)))return mp[pm(n,m)];
	LL i,x,la;
	if(n==1){
		for(x=(m*(m+1)/2)%M,i=2;i<=m;i=la+1)la=m/(m/i),x=(x-P(1,m/i)*(la-i+1)%M+M)%M;
		return mp[pm(n,m)]=x;
	}
	if(u[n]){
		for(i=1,x=0;i*i<=n;i++)if(n%i==0)if(x=(x+phi[n/i]*P(i,m/i))%M,i*i!=n)x=(x+phi[i]*P(n/i,m/(n/i)))%M;
		return mp[pm(n,m)]=x;
	}
	return (n/to[n])*P(to[n],m)%M;
}
int main(){
	for(p[0]=phi[1]=u[1]=1,i=2;i<N;i++){
		if(!f[i])p[++t]=i,phi[i]=i-1,u[i]=-1;
    	for(j=1;j<=t&&i*p[j]<N;j++){
       		f[i*p[j]]=1;
        	if(i%p[j]==0){u[p[j]*i]=0;phi[i*p[j]]=phi[i]*p[j];break;}
        	phi[i*p[j]]=phi[i]*(p[j]-1);u[p[j]*i]=-u[i];
    	}
	}
	for(i=1;i<=100000;i++)if(u[i]==0){
		for(j=1;j*j<=i;j++)if(i%j==0)if(u[i/j]){to[i]=i/j;break;}
		if(!to[i])for(j=1;j*j<=i;j++)if(i%j==0)if(u[j])to[i]=j;
	}
	for(i=1;i<N;i++)sm[i]=(phi[i]+sm[i-1])%M;
	for(scanf("%d%d",&n,&m),i=1;i<=n;i++)ans=(ans+P(i,m))%M;
	printf("%lld\n",(ans+M)%M);
}

BZOJ3561 设n<=m，=。

枚举d，然后暴力得到和，时间复杂度O(nlgn)。

#include<bits/stdc++.h>
#define W 505050
#define P 1000000007
using namespace std;typedef long long LL;int n,m,i,j,t,d,N,M,p[W],u[W];bool f[W];LL A,w,o,v[W],V[W];
LL pow(LL a,LL b,LL p){for(o=1;b;a=a*a%p,b>>=1)if(b&1)o=o*a%p;return o;}
int main(){
	scanf("%d%d",&n,&m);if(n>m)swap(n,m);
	for(u[1]=1,i=2;i<=n;i++){
		if(!f[i])p[++t]=i,u[i]=-1;
		for(j=1;j<=t&&i*p[j]<=n;j++){f[i*p[j]]=1;if(i%p[j]==0)break;u[i*p[j]]=-u[i];}
	}
	for(i=1;i<=m;i++)v[i]=1;
	for(d=1;d<=n;A=(A+w*pow(d,d,P))%P,d++){
		for(N=n/d,M=m/d,i=1;i<=M;i++)v[i]=v[i]*i%P,V[i]=(v[i]+V[i-1])%P;
		for(w=0,i=1;i<=N;i++)if(u[i])w=(w+v[i]*v[i]%P*V[N/i]%P*V[M/i]%P*u[i]+P)%P;
	}printf("%lld",A);
}

待做：3434、3601

相关文章推荐
全局相关文章

[回复]

nbdhhzh 说:
2015年6月16日 07:52

莫比乌斯函数只是把nlogn的大力容斥变成了O(n)而已。。
不过如果有修改什么的他非常有用

lbn187's Blog

莫比乌斯反演

lbn187

标签云

分类

猜你喜欢

日历

存档

最新评论

最新留言

MUSIC

膜拜

Hello World

计数器

二月
日	一	二	三	四	五	六
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29