置换群与Póyla定理
一直想研究一下可爱的置换，但是蒟蒻数学水平极低，意志力极差，当看到这些复杂的定义时，就失去了看下去的勇气
有一天翻论文的时候看到了cenbo对置换的初步研究，看到了研究置换的一丝希望
但是由于蒟蒻水平实在太低，还是没有搞懂置换究竟是什么东西，更别提Póyla定理了
今天想到家里还放了一本黑书，上面对置换的研究似乎没看过，于是翻开来看看，竟然一下子就把置换搞懂了，顺便学了下Burnside引理和Póyla定理
可爱的置换
n个元素1,2,…,n的一个置换为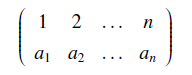
，其中a1,a2……,an互不相同且为1-n中一个整数
表示1被a1取代，2被a2取代，……,n被an取代
然后可爱的置换之间可以连接运算，如：
然后置换又是可以循环的，如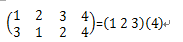
置换的循环节数就是循环的个数，如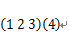
的节数是2
置换的应用
BZOJ1119：对于一个1-N的排列(ai)，每次你可以交换两个数ax与ay(x<>y)，代价为W(ax)+W(ay) 若干次交换的代价为每次交换的代价之和。请问将(ai)变为(bi)所需的最小代价（ai<>bi)是多少
如：n=6,a={1,4,5,3,6,2},b={5,3,2,4,6,1}，则可以分解为三个循环(1,5,2)(4,3)(6)的乘积，每个循环相互独立
对一个循环i，其长度为ki,因为ai<>bi，所以每个至少交换ki-1次。
一个较好的方法是让循环中代价最小的元素ti参与所有的交换，其他元素各只参加一次，总代价为sumi+(ki-2)ti，sumi为循环i中所有数的和
还有一个方法，让所有数中代价最小的元素min和ti交换，让min进入循环和ki-1个元素交换，最后再把min和ti交换，这样的代价是suni+ti+(ki+1)min
#include<cstdio>
#include<algorithm>
#define N 1001000
#define inf 1e9
using namespace std;typedef long long LL;LL sum,ans;
int n,i,p,top,sz,miv,now,a[N],b[N],c[N],w[N],num[N];bool v[N];
int main(){
scanf("%d",&n);miv=inf;
for(i=1;i<=n;i++)scanf("%d",&w[i]),miv=min(miv,w[i]);
for(i=1;i<=n;i++)scanf("%d",&a[i]);
for(i=1;i<=n;i++)scanf("%d",&b[i]),num[b[i]]=i;
for(i=1;i<=n;i++)a[i]=num[a[i]],c[num[i]]=w[i];
for(i=1;i<=n;i++)if(!v[i]){
for(now=inf,sum=0,v[p=i]=sz=1;!v[a[p]];v[p=a[p]]=1)sz++,sum+=(LL)c[p],now=min(now,c[p]);
sum+=(LL)c[p],now=min(now,c[p]);
ans+=min(sum+(LL)(sz-2)*now,sum+(LL)now+(LL)miv*(sz+1));
}
printf("%lld",ans);
}
Burnside引理
现在有n*n个小置换站在n*n的方格上，但是分不出他们的性别，问有多少种不同的性别排列方案（经过顺时针旋转性别排列相同的方案，记为一种方案）
当n=2时，很明显有6种本质不同的方案
对于四个格子1,2,3,4，有四种置换（扭脖方法）
不扭脖子：
顺时针扭一下：
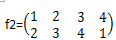
顺时针扭两下：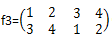
逆时针扭一下：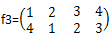
记C(f)为在置换f下保持不变的着色方案个数，那么可以证明：“本质不同的着色方案数为所有置换f的C(f)值得平均数。
| 置换 | 含义 | C(f)（该置换下不变的方案数） | |
| f1 | 不扭脖子 | 16 | |
| f2 | 顺时针扭一下 | 2 | |
| f3 | 顺时针扭两下 | 4 | |
| f4 | 逆时针扭一下 |
2 |
而所有C (f)的平均数为(16+2+4+2)/4=6,和手算结果一致
而这样直接计算复杂度是O(nsp)的，n为着色方案个数,s为置换个数,p为格子数，下面可以用Póyla定理优化
Póyla定理
用m(f)表示置换f的循环节数，如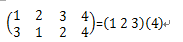的节数是2
定理：如果用k种颜色给有限集S着色，那么对于一个置换(f)，在该置换下不变的置换方案数C(f)=km(f)
| 置换 | 含义 | 循环分解式 | m(f)（f的循环节） |
| f1 | 不扭脖子 | (1)(2)(3)(4) | 4 |
| f2 | 顺时针扭一下 | (1 2 3 4) | 1 |
| f3 | 顺时针扭两下 | (1 3)(2 4) | 2 |
| f4 | 逆时针扭一下 | (1 4 3 2) |
1 |
因此不同的方案数为(24+21+22+21)/4=6,直接把该定理带入Burnside引理，可得Póyla定理
用Poyla定理可以在O(ps)的复杂度下解决着色方案记数问题
BZOJ1004
利用Burnside引理，可知本质不同的染色方案数是对于每种置换不变元素个数的平均值。
题中有m种洗牌方案加上初始状态共m+1个置换，只需对每个置换求出对于该置换不变元素的个数即可
对于每个置换中的循环，他们肯定是一个元素，设x表示在第x个循环,i,j,k表示红色、蓝色、绿色的剩余数量,du[x]表示第x个循环长度
于是可以得DP方程：dp[x][i][j][k]=dp[x-1][i-du[x]][j][k]+dp[x-1][i][j-du[x]][k]+dp[x-1][i][j][k-du[x]]
就是一个三维背包，[x]这一维可以不开，不过背包好像不太会写了呢、、
最后要求(a/b)%p，因为p为质数，所以gcd(b,p)=1,利用扩展欧几里得求出b*x%p=1的x，答案即为a*x%p
#include<cstdio>
#include<cstring>
using namespace std;
int s1,s2,s3,m,p,n,i,j,top,ans,x,y,MOD,d[66],a[66][66],f[22][22][22];
bool vis[66];
void exgcd(int a,int b,int &x,int &y){
if(!b){x=1;y=0;return;}
exgcd(b,a%b,x,y);
int t=x;x=y;y=t-a/b*y;
}
int dp(int x){
top=0;memset(vis,0,sizeof(vis));memset(f,0,sizeof(f));
for(int i=1;i<=n;i++)if(!vis[i]){
vis[p=i]=1;d[++top]=1;
while(!vis[a[x][p]]){
d[top]++;
p=a[x][p];
vis[p]=1;
}
}
f[0][0][0]=1;
for(int x=1;x<=top;x++)
for(int i=s1;i>=0;i--)
for(int j=s2;j>=0;j--)
for(int k=s3;k>=0;k--){
if(i>=d[x])f[i][j][k]=(f[i][j][k]+f[i-d[x]][j][k])%MOD;
if(j>=d[x])f[i][j][k]=(f[i][j][k]+f[i][j-d[x]][k])%MOD;
if(k>=d[x])f[i][j][k]=(f[i][j][k]+f[i][j][k-d[x]])%MOD;
}
return f[s1][s2][s3];
}
int main(){
scanf("%d%d%d%d%d",&s1,&s2,&s3,&m,&MOD);
n=s1+s2+s3;
for(i=1;i<=m;i++)for(j=1;j<=n;j++)scanf("%d",&a[i][j]);
m++;for(i=1;i<=n;i++)a[m][i]=i;
for(i=1;i<=m;i++)ans=(ans+dp(i))%MOD;
exgcd(m,MOD,x,y);
while(x<0)x+=MOD;
printf("%d",ans*x%MOD);
}
2015年6月09日 14:11
妈的你很大么。。
2019年5月27日 18:25
romantic status video download If you want to download Status then you can easily go to this website and I can use this site whenever I need it.
2019年5月31日 17:53
Romantic status video download If you want to download Status then you can easily go to this website and I can use this site whenever I need it.
2019年9月12日 15:48
By means of almost a decade of connection with trusted, good, residential place cleaning, Tyloz Place Cleaning Offerings Dubai feature residential housecleaning services who are trusted just by many and additionally known for the outstanding superior quality and maintenance. Our high quality Cleaners and additionally full Place Cleaning Offerings are first rate.
2019年11月13日 15:41
Introduce an innovative tablet or dvd movie to the class for “circle point in time, ” such as, and let the students mutually examine and inquire about it all. Create business opportunities for reserved use, posting, or collective projects implementing tech solutions.
2020年3月18日 20:07
Many of us mistakenly believe that it is technology which inturn drives uniqueness. Yet belonging to the definitions earlier, that is without a doubt clearly false. It is without a doubt opportunity which inturn defines uniqueness and concept which will allow innovation. Look into the old classic "Build a more suitable mousetrap" case study taught in every business academic institutions.
2020年3月18日 20:08
With the sports environment, peak capabilities in sports is actually a much recognized state as a result of players and even coaches in all levels. Your own home athletes can be school young boys soccer online players or Olympians striving with regard to Gold medals, pinnacle performance on sports contains always lured athletes and even coaches similarly.
2020年3月18日 20:08
This really literally true when considering buying home. To turn into a first-time residential buyer, you must know where and learn how to begin the domestic buying system. The soon after questions not to mention answers are generally carefully selected we could a facial foundation of basic knowledge of home ordering.
2020年3月18日 20:08
If your primary home inspector discovers an essential problem an specific Inspection may well be recommended. It's a wise decision to consider getting the home inspected for ones presence of many health-related negative aspects like radon air asbestos, or possible complications with the the water or misuse disposal structure.
2020年3月18日 20:09
Vacuuming cloths commonly are not the basically cleaning materials that made with the help of microfiber. Should you wish to replace your personal cleaning fabrics with microfiber, you can do which means. This will complete a whole system that wont only make your generating looking tidy, but even smelling tidy.
2020年4月28日 18:47
You'll also be given the career of safekeeping a groom's ring while in the ceremony, when also a bride's arrangement. You has to know that the absolute right place for you is due to the benefiting from line. Following on from the wedding vows, you need to sign a marriage certificate and turn into a are witness to. You also need to be the perfect man's partner while in the first ceremonial flow. But never need outshine a bride.
2020年4月28日 18:47
Relating to painting your own house, there is certainly something thinking about. Painting, by countless people's word is simple, however numerous others would argue on the fact that. When you're on the lookout to paint your place, you must always aim for the ideal person to your business. Professional assistance can turn the ideas for painting experience together.
2021年6月06日 20:09
Which means that, get wonderfully clean premises just by following certain essential specialized advice. Together with, when it arrives at getting a good top-rated house cleaning, Maid Agent Dubai delivers the best place cleaners available you one of the best bet. What is more, they know how to find satisfactory maintenance results conveniently.